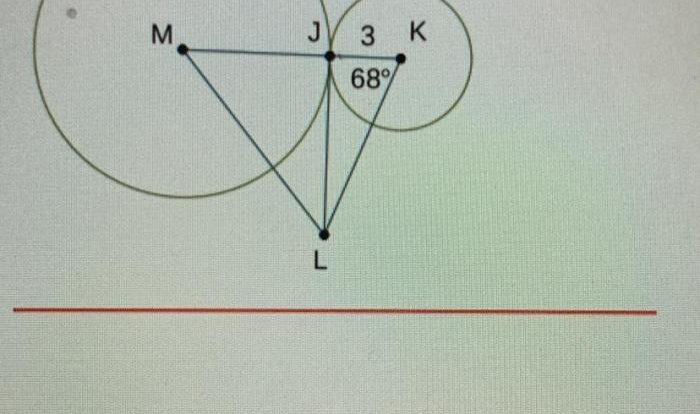
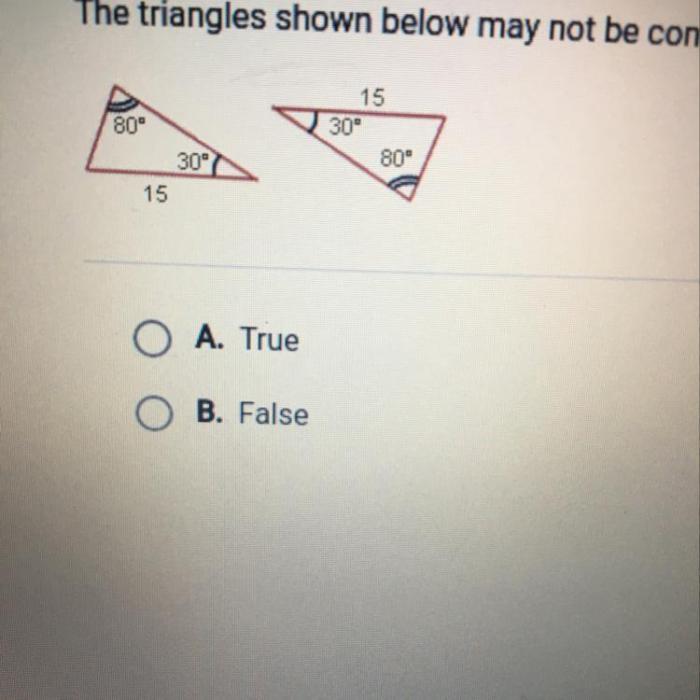
The triangles shown below may not be congruent – In the realm of geometry, the concept of triangle congruence plays a pivotal role in determining the equality of triangles. However, not all triangles are created equal, and understanding the nuances of congruence is crucial for unraveling the mysteries of geometric shapes.
This comprehensive exploration delves into the intriguing world of triangle congruence, examining the fundamental properties, theorems, and applications that govern these geometric entities. By scrutinizing the triangles shown below, we embark on a journey to decipher their congruent and non-congruent nature, unlocking the secrets that lie within their angles and sides.
Congruent Triangles: The Triangles Shown Below May Not Be Congruent
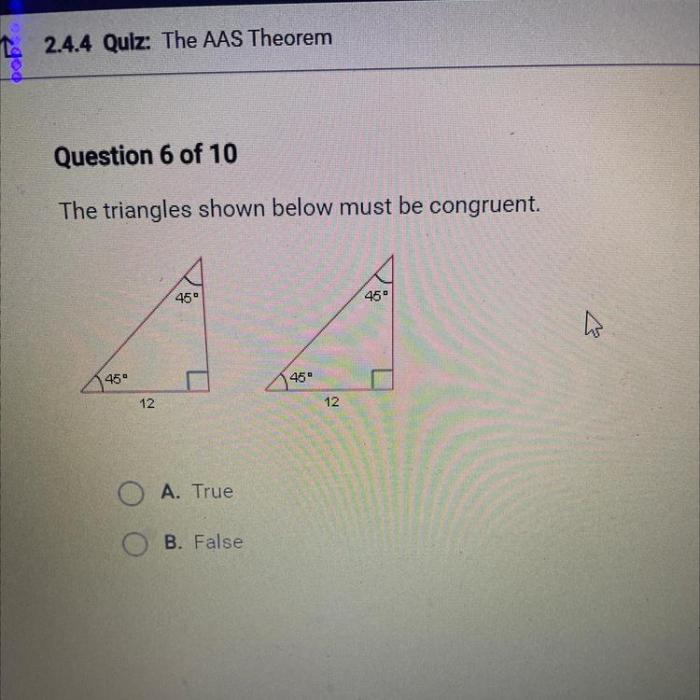
Congruent triangles are two or more triangles that have the same shape and size. This means that they have the same three sides and the same three angles.
There are a number of properties that are shared by all congruent triangles. These properties include:
- The corresponding sides of the triangles are equal in length.
- The corresponding angles of the triangles are equal in measure.
- The triangles have the same area.
- The triangles have the same perimeter.
Congruent triangles can be used to solve a variety of problems. For example, they can be used to find the missing side of a triangle, the missing angle of a triangle, or the area of a triangle.
Triangle Congruence Theorems
There are a number of different triangle congruence theorems that can be used to determine if two triangles are congruent. These theorems include:
- SSS (Side-Side-Side) Theorem:If the three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
- SAS (Side-Angle-Side) Theorem:If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
- ASA (Angle-Side-Angle) Theorem:If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.
- AAS (Angle-Angle-Side) Theorem:If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the two triangles are congruent.
- HL (Hypotenuse-Leg) Theorem:If the hypotenuse and a leg of one right triangle are equal to the hypotenuse and a leg of another right triangle, then the two triangles are congruent.
Similarity and Congruence
Similar triangles are two or more triangles that have the same shape but not necessarily the same size. This means that they have the same three angles, but their sides are not necessarily equal in length.
Congruent triangles are a special case of similar triangles. All congruent triangles are similar, but not all similar triangles are congruent.
There are a number of ways to determine if two triangles are similar. These methods include:
- AA Similarity Theorem:If two angles of one triangle are equal to two angles of another triangle, then the two triangles are similar.
- SSS Similarity Theorem:If the ratios of the corresponding sides of two triangles are equal, then the two triangles are similar.
- SAS Similarity Theorem:If the ratios of two sides and the included angle of one triangle are equal to the ratios of two sides and the included angle of another triangle, then the two triangles are similar.
Triangle Inequality Theorem
The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
This theorem can be used to determine if three given lengths can form a triangle. If the sum of the lengths of any two of the given lengths is less than or equal to the length of the third given length, then the three lengths cannot form a triangle.
Non-Congruent Triangles
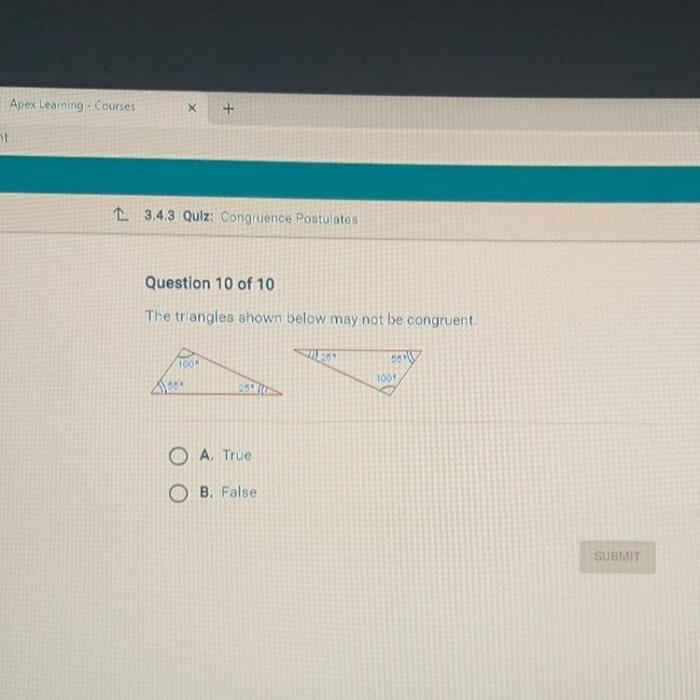
There are many different types of non-congruent triangles. Some examples of non-congruent triangles include:
- Triangles with different side lengths
- Triangles with different angle measures
- Triangles with different shapes
Non-congruent triangles can be used to solve a variety of problems. For example, they can be used to find the area of a triangle, the perimeter of a triangle, or the missing side of a triangle.
Applications of Triangle Congruence
Triangle congruence has a wide range of applications in various fields, including:
- Engineering:Triangle congruence is used to design and build structures such as bridges, buildings, and airplanes.
- Architecture:Triangle congruence is used to design and build buildings and other structures.
- Surveying:Triangle congruence is used to measure land and determine property boundaries.
- Navigation:Triangle congruence is used to determine the location of a ship or aircraft.
Helpful Answers
What is the difference between congruent and similar triangles?
Congruent triangles are triangles that have the same shape and size, while similar triangles have the same shape but not necessarily the same size.
How can I determine if two triangles are congruent?
You can use the triangle congruence theorems (SSS, SAS, ASA, AAS, HL) to determine if two triangles are congruent.
What is the triangle inequality theorem?
The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.