Which of the following subsets of are subspaces of? The concept of a subspace in linear algebra is fundamental, and understanding its properties is crucial. This exploration delves into the conditions that define a subspace, examining examples and applications across various mathematical disciplines.
Subspaces are subsets of vector spaces that inherit the vector space structure, allowing for operations like vector addition and scalar multiplication. This exploration unveils the characteristics that distinguish subspaces from mere subsets, empowering readers to confidently identify and utilize subspaces in their mathematical endeavors.
Subspaces: Which Of The Following Subsets Of Are Subspaces Of

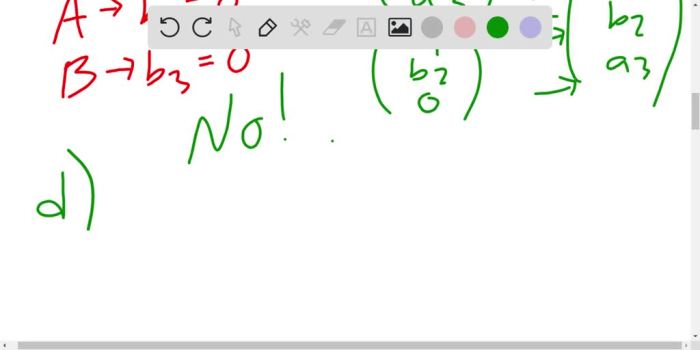
In linear algebra, a subspace of a vector space is a non-empty subset that is closed under vector addition and scalar multiplication. This means that if uand vare vectors in the subspace, then u+ vand cuare also in the subspace for any scalar c.
Subspaces are important in linear algebra because they allow us to decompose vector spaces into smaller, more manageable pieces. They also play a role in many applications of linear algebra, such as linear transformations, matrix theory, and differential equations.
Examples of Subspaces
- The zero subspace: This is the subspace consisting of the zero vector only.
- The entire vector space: This is a subspace of itself.
- The subspace spanned by a set of vectors: This is the smallest subspace that contains all of the vectors in the set.
- The null space of a linear transformation: This is the subspace of the domain of the transformation that is mapped to the zero vector.
- The column space of a matrix: This is the subspace of the codomain of the matrix that is spanned by the columns of the matrix.
Conditions for Subspaces
In order for a subset of a vector space to be a subspace, it must satisfy the following conditions:
- It must contain the zero vector.
- It must be closed under vector addition.
- It must be closed under scalar multiplication.
If a subset satisfies these conditions, then it is a subspace of the vector space.
Applications of Subspaces, Which of the following subsets of are subspaces of
Subspaces have many applications in different areas of mathematics, including:
- Linear transformations: Subspaces can be used to decompose linear transformations into smaller, more manageable pieces.
- Matrix theory: Subspaces can be used to find the eigenvalues and eigenvectors of a matrix.
- Differential equations: Subspaces can be used to solve systems of differential equations.
FAQ Explained
What is the primary condition for a subset to be a subspace?
A subset is a subspace if it is closed under vector addition and scalar multiplication.
Can a subspace have a different dimension than the original vector space?
No, a subspace must have the same dimension as the original vector space.
What are some applications of subspaces in linear transformations?
Subspaces are used to find the null space and column space of a linear transformation, which are important for solving systems of linear equations.